重力选煤工艺效果的评定
1. 可能偏差与不完善度
可能偏差和不完善度是国际评定重选作业效率的通用标准,已为许多国家所釆用。
2. 数量效率
数量效率指标是一种相对效率。它是指灰分相同时,精煤实际产率和理论产率的 比值。是生产、技术管理中的一个重要指标。但该指标的试验与计算工作量均较大,不 能及时指导生产。精煤理论产率可以从原煤可选性曲线上求出。数量效率和可能偏差一样,是使用 得较多的一个指标。
3. 错配物总量
物料分选或分级时,混入各产品中非规定成分的物料称为错配物。特鲁姆普把它 们称为“迷路的精煤”、“迷路的矸石”等等。等误密度指 在两重选产品中,错配物相等时的密度。等误密度用符号“!”表示。
错配物总量能较为明确地表达出物料分选的结果及设备的潜力。试验与计算的工 作量也较少。在日常检查中可用占产品的百分数来表达(即污染指标或快速浮沉指 标),分选密度釆用接近理论分选密度的数值,密度级差取0.05 g/cm3。理论分选密度: 即相应于分选过程中获得的实际灰分的产品,从密度曲线上查得的相应密度。若理论 分选密度用符号表示。则
Se = St-0.05 (8-27)
在原煤可选性变化不大的情况下,只要注意分选密度的一致性,就可以把日常检 查、月综合、年度检查等结果联系对比加以分析,具有对比性。故用此指标指导生产比数量效率方便。
例如,根据表8-12资料计算产物错配物指标。 第一步:列表计算各密度级的错配物数量,见表8-13。
表8-13错配物数量计算表
|
|
高密度分割 |
低密度分割 |
||||||||||
|
|
数量/% |
|
错配量/% |
数量/% |
|
错配量/% |
||||||
|
密度 级别 /g,cm-3 |
精煤 |
|
密 |
精煤+ |
矸石 |
|
|
|
密 |
精煤 |
中煤 |
|
|
+ |
矸石 |
中煤中 |
中的 |
合计 |
精煤 |
中煤 |
中的 |
中的 |
合计 |
|||
|
中煤 |
|
|
的沉物 |
浮物 |
|
|
|
|
沉物 |
浮物 |
|
|
|
表 8-12 (11) |
表 8-12 (5) |
度 |
(2) |
(3) |
( 5) + ( 6) |
表 8-12 (9) |
表 8-12 (7) |
度 |
(8) |
( 9) |
(11)+ (12) |
|
|
|
||||||||||||
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
(11) |
(12) |
(13) |
|
-1.3 |
21.92 |
0.21 |
|
68.90 |
0.00 |
68.90 |
18.20 |
3.72 |
|
50.40 |
0.00 |
50.40 |
|
1.3〜1.4 |
28.23 |
0.37 |
1.3 |
46.98 |
0.21 |
47.19 |
22.62 |
5.61 |
1.3 |
32.20 |
3.72 |
35.92 |
|
1.4〜1.5 |
10.32 |
0.28 |
1.4 |
18.75 |
0.58 |
19.33 |
6.94 |
3.38 |
1.4 |
9.58 |
9.33 |
18.91 |
|
1.5〜1.6 |
4.43 |
0.76 |
1.5 |
8.43 |
0.86 |
9.29 |
1.96 |
2.47 |
1.5 |
2.64 |
12.71 |
15.35 |
|
1.6〜1.8 |
2.63 |
2.52 |
1.6 |
4.00 |
1.62 |
5.62 |
0.57 |
2.06 |
1.6 |
0.68 |
15.18 |
15.86 |
|
+ 1.8 |
1.37 |
26.96 |
1.8 |
1.37 |
4.14 |
5.51 |
0.11 |
1.26 |
1.8 |
0.11 |
17.24 |
17.35 |
|
|
|
|
|
0.00 |
31.10 |
31.10 |
|
|
|
0.00 |
18.50 |
18.50 |
第二步:绘制错配物曲线。
根据表8-13中第4、5栏和第4、6栏数据绘制高密度分割错配物曲线:污染曲线 和损失曲线,见图8-19。
由图8-19可查出高密度分割时错配物指标为:
分选密度Sp1 = 1.71 g/cm3时,轻产品中的错配量mh = 2.0% ;重产品中的错配量 !]=3.1% ;错配物总量 m0 = 5.1%。
等误密度<5e1 = 1.67 g/cm3时,轻产品中的错配量mh = 2.6%;重产品中的错配量 mj =2.6% ;错配物总量 m0 = 5.2%。
重力选矿工艺效果的评定
通常用以判断重力选矿工艺分选过程(也包括筛分、分级等其他分离过程)效果的 指标有回收率e、品位廿、产率八金属量$、富矿比和选矿比等。但是其中任一指标,都 不能同时从数量和质量两个方面反映选矿过程的效率。例如,回收率和金属量是数量 指标,品位和富矿比是质量指标;但产率和选矿比若不同其他指标连用,根本不能说明 问题。故在实际工作中,通常都是一个数量指标与一个质量指标连用。
但是如用一对指标作判据常常出现不易分辨的情况例如,两个试验,一个品位较高 而回收率较低,另一个品位较低而回收率较高,就难以评定它们结果的优劣。为此,长 期以来不少人致力于寻求一个综合指标来代替一对指标作判据的方法,为此提出了各 式各样的效率公式。可是,由于选矿工艺遇到的各种具体情况。对分选效率在数量方 面和质量方面的要求,往往有不同的侧重,故也无法找到能反映这种不同要求的灵活的 理想公式。因此,与重力选煤工艺效果的评定一样,只得釆取在不同情况下,选择不同 的判据,并在利用某一综合指标为主要判据的同时,再选用一两个质量指标和数量指标 作为辅助指标。
釆用图解的方法也可评定选矿效率。所谓图解法,其实质也是利用一对指标作判据,但可利用图中曲线推断出,当其中一个指标相同时,另一个指标是高是低,因而不会 出现不易比较的情况。用图解法评定选矿工艺效果的一个重要实例,是分配曲线法。
总之,重力选矿工艺效果的评定,与选煤一样,都是釆用两种基本方法,一是选矿效 率的计算,另一是利用分配曲线的特性参数。
1.选矿效率的计算
(1)质量效率(简称质效率)指标
例如,某黄铜矿石,理论上可达到的最高精矿品位,是纯黄铜矿含铜量,即!#% ) 34.5%Cu,若实际精矿品位! = 25%Cu,应该可以满意;而辉铜矿矿石,理论最咼品位应 是纯辉铜矿的含铜量,即!m必= 79.8%Cu,如实际精矿! = 25%Cu,则说明选矿效率太 低了。显然,若只用!作为分选过程质量效率的判据,是不合适的,故用!与!ma%的比 值。
但是,若原矿品位为«,那么即使是一个简单的分样过程,毫无分选作用,精矿品位 !也不会等于0,而是等于a,当然,这决不会被看做反映了选矿过程的质效率。因此, 提出用(!-a)代替!作为度量分选过程的质效率。这时,前述分样过程! = a,!-a )0。显然,如以(!-a)作为质效率指标,对于分样过程来说,其分选的质效率为0。
(3)综合效率
计算分选(包括分级)过程的综合效率公式,可以分成两类:第一类是以1918年美 国学者R.T.汉考克所提出的分离效率公式为代表;第二类则是以弗来敏一斯梯芬斯 公式和道格拉斯公式为代表。
a、、——分别代表原矿、精矿及尾矿中有用矿物的含量。
由于实际生产或试验工作中获得的品位数据一般均为元素(或化合物)含量,故利用上式时,应预先将化验品位换算为矿物含量,
右田矿瑜不旦 该产品中有用元素(或化合物)的含量
有用矿物含量=纯有用矿物中有用元素(或化合物)的含量"100% 故若以爲表示纯矿物中有用元素(或化合物)含量,则只要将上述公式中含量指标均 除以!%/100,即可直接按化验品位计算分选效率平 此时,式(8-30)则变换成:
” (a - $)(! - $)_ " 100%
"-(!-$)(#- a/!%)倾%
可见,这类综合效率公式推导的指导思想,不仅考虑有用成分在精矿中的回收率, 而且还考虑无用成分在精矿中的混杂率,设法从''有效回收率”中扣除''无效回收率”的 影响。这样便使综合效率公式既反映过程的量效率,又反映过程的质效率。
2.图解法评定分选效率
利用分配曲线评定分选的工艺效果,是图解法中的一个重要方法。
用于重力选矿过程工艺效果的评定,但也可以用于磁选(磁性组分的分配)、分级(粒度 组分的分配)等。它的主要优点是最终判据为单一数据,容易得出明确结论。分配曲线
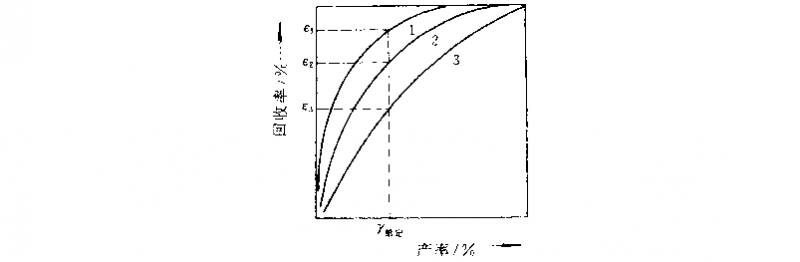
图8-21 % = ( y)关系曲线
在一般场合下,也可以利用下列方法作图来评价分选效果。首先将每个待比方案 釆用分批截取与产率!的关系曲线及回收率e与精矿品位f的关系曲线等。这时再看哪一个方案的 曲线位置比较高,那么它的分选效果必然也较好。例如在e =( !)图上(即图8-21), 曲线位置较高,意味着在给定的相同精矿产率下,回收率e较高,既然产率相同,e较高 则精矿品位f也必然较高;而在"=(辭图(即图8-22)中,曲线位置较高表明在相同 的给定精矿品位时e较高。
免责声明:矿库网文章内容来源于网络,为了传递信息,我们转载部分内容,尊重原作者的版权。所有转载文章仅用于学习和交流之目的,并非商业用途。如有侵权,请及时联系我们删除。感谢您的理解与支持。